Various Forms of the Equation of a Line

The equations of the normal to the curve  $x=1-\cos \theta :y=\theta -\sin \theta$ at $\theta =\frac{\pi }{4}$  would be:

The diagram shows the graph of three linear functions, $g,f$ and $h$ are in the colour green, blue and red respectively.

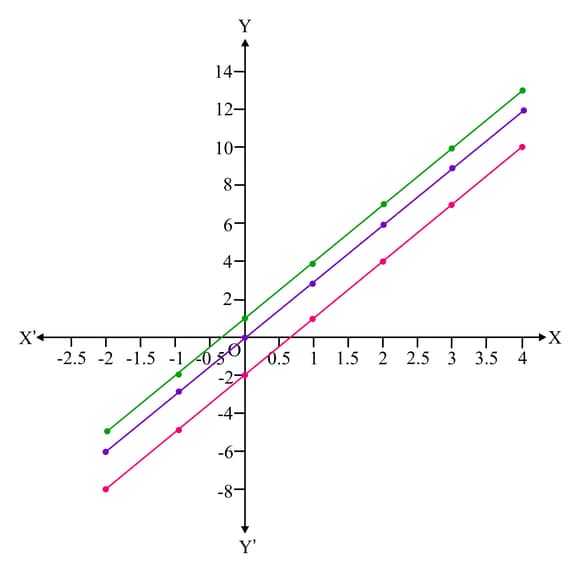
Find the equation for each of the functions.

The three functions are antiderivative of $y=f\left(x\right)$

A Canadian bank charges its customers a fixed commission fee of $\$$ $a$ Canadian dollars (CAD) if they wish to exchange CAD into euros $\left(\epsilon \right)$.

The bank then uses the exchange rate $\$1:\epsilon r$ to convert the remaining amount.

Michael converts $1200$ CAD and receives $\epsilon 765$ from the bank.

Janet exchanges $500$ CAD and receives $\epsilon 315$ from the same bank.

If Michael and Janet had put their Canadian dollars together first and then exchanged it all in one transaction, calculate the amount in euros, to the nearest cent, that they would have received.  If they receive $k$ euros, then the value of $k$ is  ..... (Round off and write up to $2$ decimal places)

A Canadian bank charges its customers a fixed commission fee of $\$$ $a$ Canadian dollars (CAD) if they wish to exchange CAD into euros $\left(\epsilon \right)$.

The bank then uses the exchange rate $\$1:\epsilon r$ to convert the remaining amount.

Michael converts $1200$ CAD and receives $\epsilon 765$ from the bank.

Janet exchanges $500$ CAD and receives $\epsilon 315$ from the same bank.

Find the value of $r$. (Round off and write up to $3$ decimal places)

A Canadian bank charges its customers a fixed commission fee of $\$$ $a$ Canadian dollars (CAD) if they wish to exchange CAD into euros $\left(\epsilon \right)$.

The bank then uses the exchange rate $\$1:\epsilon r$ to convert the remaining amount.

Michael converts $1200$ CAD and receives $\epsilon 765$ from the bank.

Janet exchanges $500$ CAD and receives $\epsilon 315$ from the same bank.

Find the value of $a$. (Round off and write up to $3$ decimal places)

The swimming pool at West Park contains $500000$ litres of water when it is full. The pool can be drained of water at a constant rate of $50000$ litres per hour.

Write an equation for the volume $(V \mathrm{litres})$ of water remaining in the pool $t$ hours since draining began.

At $8:00 \mathrm{am}$ the pool is full fo water and the drain is opened.

The swimming pool at East Park contains $800000$ litres of water when it is full, and can be drained at a rate of $100000$ litres per hour. At $8:00 \mathrm{am}$ (when the drain is opened at West Park pool), the drain is also opened at the East park pool.

Calculate the time when the pool at West Park contains the same amount of water as the pool at East Park. Find also the volume of water in each pool at this time.

The swimming pool at West Park contains $500000$ litres of water when it is full. The pool can be drained of water at a constant rate of $50000$ litres per hour.

Write an equation for the volume $(V \mathrm{litres})$ of water remaining in the pool $t$ hours since draining began.

At $8:00 \mathrm{am}$ the pool is full fo water and the drain is opened.

Determine the time when the pool is $25\%$ full of water.

The swimming pool at West Park contains $500000$ litres of water when it is full. The pool can be drained of water at a constant rate of $50000$ litres per hour.

Write an equation for the volume $(V \mathrm{litres})$ of water remaining in the pool $t$ hours since draining began.

The coordinates of point $P$ are $\left(-3, 8\right)$ and the coordinates of point $Q$ are $\left(5, 3\right)$. $M$ is the midpoint of $\left[PQ\right]$.

$L_1$ is the line which passes through $P$ and $Q$.

The line $L_2$ is perpendicular to $L_1$ and passes through $M$.

Write down in the form $y=mx+c$, the equation of $L_2$.

Three farmhouses are to be powered by wind. The farms are located at $A\left(60, 20\right), B(220, 120)$ and $C\left(240, 40\right)$, where the coordinates are in metres. A wind turbine is to be placed at the point equidistant from the farms $A, B$ and $C$. Find the equation of the line $\left(BC\right)$.

Three farmhouses are to be powered by wind. The farms are located at $A\left(60, 20\right), B(220, 120)$ and $C\left(240, 40\right)$, where the coordinates are in metres. A wind turbine is to be placed at the point equidistant from the farms $A, B$ and $C$. Find the equation of the line $\left(AC\right)$.

Maria works as a part-time waitress in the summer and earns $\$30$ per day plus $2\%$ of all food and drink sales for the day. Write an equation to represent her daily earnings, $A$, in USD, in relation to the amount, $x$, in USD, of all sales of food and drinks during the day. Find what Maria's earnings would be if the amount of food and drinks sold during a certain day were $\$2400.$

Maria works as a part-time waitress in the summer and earns $\$30$ per day plus $2\%$ of all food and drink sales for the day. Write an equation to represent her daily earnings, $A$, in USD, in relation to the amount, $x$, in USD, of all sales of food and drinks during the day. Determine the $y$-intercept.

Maria works as a part-time waitress in the summer and earns $\$30$ per day plus $2\%$ of all food and drink sales for the day. Write an equation to represent her daily earnings, $A$, in USD, in relation to the amount, $x$, in USD, of all sales of food and drinks during the day. Determine the gradient. Interpret its meaning.

Maria works as a part-time waitress in the summer and earns $\$30$ per day plus $2\%$ of all food and drink sales for the day. Write an equation to represent her daily earnings, $A$, in USD, in relation to the amount, $x$, in USD, of all sales of food and drinks during the day.

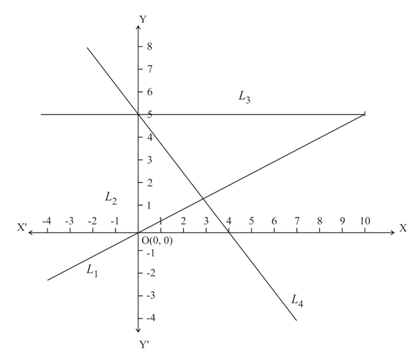
A landscape architect has planned four new paths in a park. The paths are straight lines as shown on the diagram below. Find the equations of the paths $L_1,L_2,L_3\text{ and }$$L_4$.

Albena lives in Belgium. She travels to the USA where the temperature is measured in degrees Fahrenheit. She wants to know how hot it is in ${}^{\circ }\mathrm{C}$ if the thermometer shows $83°\mathrm{F}.$

Use the fact that water boils at $100°\mathrm{C}$ and $212°\mathrm{F}\text{ , }$and that water freezes at $0°\mathrm{C}$, and $32°\mathrm{F}\text{ . }$

Write an equation for the relationship between $C$ and $F$, where $F$ represents degrees Fahrenheit and $C$ represents degrees Celsius. Write your equation in the form $F=m C+k$.